A few cinematographic tributes to mathematicians and scientists have been made for public consumption, most notably “A Beautiful Mind” about John Nash in 2001, starring Russell Crowe. Now a new film, “The Man Who Knew Infinity,” tells about Srinivasa Ramanujan (1887-1920), starring Dev Patel (“Slumdog Millionaire”) as the lead character along with Jeremy Irons as G. H. Hardy (1877-1947) and Toby Jones as John Littlewood (1885-1977). The movie, with limited showings, is based on an eponymous biography by Robert Kanigel, published in 1991.
The film, described by Pennsylvania State professor George Andrews, tells the story of a self-taught clerk in Madras (present-day Chennai), located in southern India. At age 16, Ramanujan borrowed “A Synopsis of Elementary Results in Pure Mathematics” by George Carr. That 1886 reference included almost 5,000 theorems, which Ramanujan labored to prove. Paper being expensive, Ramanujan developed these proofs on a slate board, then transferred select formulas to a notebook.
In 1913, he wrote to Hardy, the aloof academic don at Cambridge University, for assistance. Ramanujan included some of his theorems, including this one 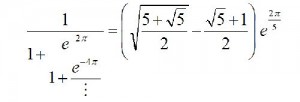
offered without proof. Hardy recognized the talent behind the author and invited him to Cambridge for collaboration. Ramanujan initially declined due to Brahmin injunctions on travel abroad, since he was a devout believer in the goddess Namagiri. Hardy arranged an appointment at the Presidency College in Madras, and after a vision Ramanujan relented.
Leaving his wife and mother behind, Ramanujan stayed in England five years, from 1914-1919. Although well-paid for his efforts, the chilly climate, scarcity of vegetarian cuisine, wartime tensions, and absence of family intensified his loneliness. His contributions however, were notably appreciated.
A Formidable Mathematical Mind
His first paper at Cambridge described series approximations to pi (π). His longest paper was devoted to properties of highly composite numbers. These are positive integers that have more divisors than any smaller positive integer. Examples and their prime factorization include the fifth: 12=22×3, tenth: 120=23×3×5, twentieth: 7,560=23×33×5×7, and so forth. The concept can be traced to Plato ,who set the ideal number of urban citizens at 5,040 (the nineteenth such number). Ramanujan received his BA, later renamed PhD, for this contribution.
One film scene adapts Hardy’s famous anecdote about the “taxicab number” that highlighted Ramanujan’s prodigious skills. The movie depicts this encounter on the street, rather than during Ramanujan’s convalescence. As Hardy relates in a 1921 article, “I remember once going to see him when he was ill at Putney. I had ridden in taxi cab number 1729 and remarked that the number seemed to me rather a dull one, and that I hoped it was not an unfavorable omen. ‘No,’ he replied, ‘it is a very interesting number; it is the smallest number expressible as the sum of two (positive) cubes in two different ways.’”
That is, 1,729 is one-cubed plus 12-cubed and also 9-cubed plus 10-cubed (or algebraically 1729=13+123=93+103). The next such numbers are 4,104, 13,832, and 20,683.
The movie’s finale centers on Ramanujan’s election as a Fellow of the Royal Society and a Fellow of Trinity College, the first Indian so honored. Returning to India’s warmer climate, Ramanujan further worked on mock theta functions (with asymptotic expansions at the cusps). His last writings were rediscovered in 1976 and published as the Lost Notebook. Unfortunately, his precarious health continued to deteriorate, and he died in 1920, possibly from hepatic amoeblasis. The film presents this melancholy announcement in a letter to Hardy.
Math Is Really Important Even If You Don’t Get It
The importance of mathematics is difficult to exaggerate, but its concepts can be decidedly non-intuitive. Ironically, our prehistoric ancestors most likely invented tally counting well before symbolic writing (and perhaps contemporaneously with cave art). The Ishango bone has notches on a baboon fibula dating from the upper Paleolithic (about 20 millennia ago). Although most ancient peoples were illiterate, the expression of numbers had importance in mutually acknowledged obligations, as mentioned in Luke 16:5-7, whether these bills were written on papyrus or potsherds.
The infrequent instances in which cinema glimpses renown genius deserve praise as illumination of achievement and inspiration to follow. Not everyone agrees. The Guardian published a review that dismisses the film for tepid efforts to explain or display the mathematics Ramanujan derived, focusing instead on personal experiences. This seems unfair to the film’s creators, as the minimum level of mathematical recognition at research levels exceeds the depths of courses many engineering and science students take, never mind what the general public understands. An example might suffice: the well-known waitress integral joke (abbreviated here).
Two mathematicians sit in a bar. The pessimist says to the optimist that the average person knows very little about basic mathematics. The optimist disagrees, and asserts that most people can cope with a reasonable amount of mathematics.
The pessimist goes to the restroom, and in his absence the optimist calls over the waitress. He tells her that after his friend has returned, he will ask her a question. All she has to do is answer “one third x cubed.” She agrees, and leaves mumbling to herself, “wun thir dex kyoobed…”
After the pessimist returns, the optimist proposes a bet to prove his point—to ask the waitress an integral, and the pessimist laughingly accepts. The optimist calls the waitress and asks her, “What is the integral of x squared?”
The waitress replies “one third x cubed” and, while walking away, turns back and mutters “plus a constant!”
Our children heard this effort at humor, but didn’t grasp its meaning until they took calculus and could distinguish between definite and indefinite integrals. Converging infinite series can seem abstract, as exemplified by Zeno’s paradox, traversing a distance in continued halves (½+¼+⅛+…) but never reaching the goal. By incrementing time in the same manner, one can deduce the speed for that travel. Mathematical prodigies pioneer solutions and proofs, but for most of us, these techniques must be conscientiously taught and laboriously learned.
“The Man Who Knew Infinity” offers a glimpse of that talent, roughly a century after Ramanujan’s tenure in England. Mathematics grants access to truth and beauty to those who can read its peculiar language and syntax. For those below the rarefied heights, mathematics provides analytical tools with which to understand the universe and manipulate its components.
Maybe such aspirations seem arrogant to those drawn to central planning through political aggrandizement. But such seekers of power desire what participants in technology provide—recall Stalin’s admonition, “Leave them alone; we can always shoot them later.” Sometimes the well-deserving receive rewards instead of the firing squad—and “The Man Who Knew Infinity” presents such a tribute.